Dialéctica de la naturaleza. Por Frederick Engels 1883

BICENTENARIO DE FEDERICO ENGELS

Matemáticas

Notas y fragmentos

Fuente : Dialéctica de la naturaleza , págs. 257-272;
Primera edición : Progress Publishers, 1934, sexta edición, 1974;
Traducido del alemán por Clemens Dutt;
Transcrito : por Andy Blunden, 2006.

[Matemáticas]

Los llamados axiomas de las matemáticas son las pocas determinaciones del pensamiento que las matemáticas necesitan para su punto de partida. Las matemáticas son la ciencia de las magnitudes; su punto de partida es el concepto de magnitud. Define esto débilmente y luego agrega las otras determinaciones elementales de magnitud, no contenidas en la definición, desde afuera como axiomas, de modo que aparecen como no probadas y, naturalmente, también como matemáticamente improbables. El análisis de magnitud produciría todas estas determinaciones de axiomas como determinaciones necesarias de magnitud. Spencer tiene razón en la medida en que se hereda lo que así nos parece la autoevidencia de estos axiomas . Son demostrables dialécticamente, en la medida en que no son puras tautologías.

* * *

Matemáticas. Nada parece tener una base más sólida que la diferencia entre las cuatro especies de operaciones aritméticas, los elementos de todas las matemáticas. Sin embargo, desde el principio se ve que la multiplicación es una suma abreviada, y la división una resta abreviada, de un número definido de magnitudes numéricas iguales; y en un caso, cuando el divisor es una fracción, la división se realiza incluso multiplicando por la fracción invertida. En el cálculo algebraico la cosa se lleva mucho más allá. Cada resta ( a – b ) se puede representar como una suma (- b + a ), cada división a / b como una multiplicación a× 1 / b. En los cálculos con potencias de magnitudes se va mucho más allá. Todas las diferencias rígidas entre los tipos de cálculo desaparecen, todo puede presentarse en forma opuesta. Una potencia se puede poner como raíz ( x ² = √x ⁴ ;), una raíz como potencia (√x = x ^½ ). La unidad dividida por una potencia o raíz se puede poner como una potencia del denominador (1 / √x = x ^-½ ; 1 / x ³ = x ^-3 )

La multiplicación o división de las potencias de una magnitud se convierte en suma o resta de sus exponentes. Cualquier número puede concebirse y expresarse como la potencia de cualquier otro número (logaritmos, y = a ^x ). Y esta transformación de una forma en la opuesta no es una nimiedad, es una de las palancas más poderosas de la ciencia matemática, sin la cual hoy en día apenas se realizan los cálculos más difíciles. Si los poderes negativos y fraccionarios solo fueran abolidos de las matemáticas, ¿hasta dónde se podría llegar?

(—.— = +, – / – = +, √-1, etc., que se expondrá antes.)

El punto de inflexión en matemáticas fue la magnitud variable de Descartes . Con eso vino el movimiento y, por lo tanto, la dialéctica en las matemáticas, y al mismo tiempo, también, necesariamente el cálculo diferencial e integral, que además comienza inmediatamente, y que en conjunto fue completado por Newton y Leibniz, no descubierto por ellos.

* * *

Cantidad y calidad. El número es la determinación cuantitativa más pura que conocemos. Pero está repleto de diferencias cualitativas. 1. Hegel, número y unidad, multiplicación, división, elevación a un poder superior, extracción de raíces. Así, y esto no se muestra en Hegel, ya hacen su aparición las diferencias cualitativas: números primos y productos, raíces simples y potencias. 16 no es simplemente la suma de 16 unidades, también es el cuadrado de 4, la cuarta potencia de 2. Aún más. Los números primos comunican cualidades nuevas y definitivamente determinadas a los números derivados de ellos mediante la multiplicación con otros números; solo los números pares son divisibles por 2, y hay una determinación similar en el caso de 4 y 8. Para 3 existe la regla de la suma de las cifras, y lo mismo para 9 y también para 6, en el último caso en combinación con el número par. Para 7 hay una regla especial. Estos forman la base de trucos con números que parecen incomprensibles para los no iniciados. De ahí lo que dice Hegel (Cantidad , pág. 237) sobre la ausencia de pensamiento en aritmética es incorrecta. Compare, sin embargo, Measure. ^[213]

Cuando la matemática habla de lo infinitamente grande y lo infinitamente pequeño, introduce una diferencia cualitativa que incluso toma la forma de una oposición cualitativa infranqueable: cantidades tan enormemente diferentes entre sí que toda relación racional, toda comparación, entre ellas cesa, que se vuelven cuantitativamente. inconmensurable. La inconmensurabilidad ordinaria, por ejemplo del círculo y la línea recta, es también una diferencia cualitativa dialéctica; pero aquí es la diferencia en cantidad de magnitudes similares lo que aumenta la diferencia de calidad hasta el punto de inconmensurabilidad.

* * *

Número. El número individual ya está dotado de calidad en el propio sistema numérico, y la calidad depende del sistema utilizado. 9 no es sólo 1 sumado 9 veces, sino también la base de 90, 99, 900.000, etc. Todas las leyes numéricas dependen y están determinadas por el sistema adoptado. En sistemas diádicos y triádicos, 2 multiplicado por 2 no es igual a 4, sino = 100 o = 11. En todos los sistemas con un número básico impar, la diferencia entre números pares e impares cae al suelo, por ejemplo, en el sistema basado en 5, 5 = 10, 10 = 20, 15 = 30. Asimismo en el mismo sistema las sumas de dígitos 3 n de productos de 3 o 9 (6 = 11, 9 = 14). Por tanto, el número básico determina no solo su propia calidad, sino también la de todos los demás números.

Con las potencias de los números, el asunto va más allá: cualquier número puede concebirse como la potencia de cualquier otro número; hay tantos sistemas logarítmicos como números enteros y fraccionarios.

* * *

Uno. Nada parece más simple que la unidad cuantitativa, y nada es más múltiple que ella, tan pronto como la investigamos en conexión con la pluralidad correspondiente y según sus diversos modos de origen a partir de la pluralidad. En primer lugar, uno es el número básico de todo el sistema numérico positivo y negativo, y todos los demás números surgen de la adición sucesiva de uno a sí mismo.

Uno es la expresión de todas las potencias positivas, negativas y fraccionarias de uno: 1 ² , √1, 1 ^-2 son todos iguales a uno.

Es el contenido de todas las fracciones en las que el numerador y el denominador resultan ser iguales. Es la expresión de todo número que se eleva a la potencia de cero, y con ello el único número cuyo logaritmo es el mismo en todos los sistemas, es decir, = 0. Así, uno es el límite que divide todos los sistemas posibles de logaritmos en dos partes: si la base es mayor que uno, entonces los logaritmos de todos los números más de uno son positivos y de todos los números menos de uno negativos; si es menor que uno, ocurre lo contrario.

Por lo tanto, si cada número contiene unidad en sí mismo en la medida en que está compuesto enteramente por unos sumados, la unidad también contiene todos los demás números en sí misma. Esto no es solo una posibilidad, en la medida en que podemos construir cualquier número únicamente de unos, sino también una realidad, en la medida en que uno es una potencia definida de todos los demás números. Pero los mismos matemáticos que, sin inmutarse, interpolan en sus cálculos, donde les conviene, x ⁰= 1, o una fracción cuyo numerador y denominador son iguales y que, por tanto, también representa a uno, que por tanto aplican matemáticamente la pluralidad contenida en la unidad, levantan la nariz y hacen muecas si se les dice en términos generales que la unidad y la pluralidad son inseparables, mutuamente conceptos penetrantes y que la pluralidad no está menos contenida en la unidad que la unidad en la pluralidad. Cuánto es este el caso lo vemos tan pronto como abandonamos el campo de los números puros. Ya en la medición de líneas, superficies y volúmenes de cuerpos se hace evidente que podemos tomar cualquier magnitud deseada del orden apropiado como unidad, y lo mismo vale para la medición de tiempo, peso, movimiento, etc. de células, incluso los milímetros y miligramos son demasiado grandes,

* * *

Cero, porque es la negación de una cantidad determinada, no está desprovisto de contenido. Por el contrario, el cero tiene un contenido muy definido. Como límite entre todas las magnitudes positivas y negativas, como único número realmente neutral, que no puede ser ni positivo ni negativo, no solo es un número muy definido, sino también más importante en sí mismo que todos los demás números limitados por él. De hecho, cero es más rico en contenido que cualquier otro número. Colocado a la derecha de cualquier otro número, le da a este último, en nuestro sistema de números, el valor diez veces mayor. En lugar de cero, se podría usar aquí cualquier otro signo, pero solo con la condición de que este signo, tomado por sí mismo, signifique cero, = 0. Por lo tanto, es parte de la propia naturaleza del cero que encuentre esta aplicación y que solo él pueda aplicarse de esta manera. El cero aniquila todos los demás números con los que se multiplica; unido con cualquier otro número como divisor o dividendo, en el primer caso lo hace infinitamente grande, en el segundo infinitamente pequeño; es el único número que se encuentra en una relación de infinito con cualquier otro número. 0/0 puede expresar todos los números entre – ∞ y + ∞, y en cada caso representa una magnitud real.

El contenido real de una ecuación surge claramente por primera vez cuando todos sus miembros se han llevado a un lado y, por lo tanto, la ecuación se reduce a un valor cero, como ya ocurre con las ecuaciones cuadráticas, y es casi la regla general en álgebra superior. La función F (x, y) = O también se puede igualar az, y esta z, aunque es = 0, se diferencia como una variable dependiente ordinaria y se determina su derivada parcial.

Sin embargo, la nada de cada cantidad está determinada cuantitativamente en sí misma, y ​​sólo por esa razón es posible calcular con cero. Los mismos matemáticos que no se sienten avergonzados de calcular el cero de la manera anterior, es decir, de operar con él como un concepto cuantitativo definido, poniéndolo en relación cuantitativa con otros conceptos cuantitativos, se agarran la cabeza con desesperación cuando leen esto en Hegel. generalizado como: la nada de un algo es una nada determinada .

Pero ahora para la geometría (analítica). Aquí cero es un punto definido desde el cual se toman medidas a lo largo de una línea, en una dirección positiva, en la otra negativa. Aquí, por lo tanto, el punto cero no solo tiene tanta importancia como cualquier punto denotado por una magnitud positiva o negativa, sino una importancia mucho mayor que todos ellos: es el punto del que todos dependen, del que son todos relacionados, y por los cuales todos están determinados. En muchos casos, incluso se puede tomar de forma bastante arbitraria. Pero una vez adoptado, sigue siendo el punto central de toda la operación, a menudo determinando incluso la dirección de la línea a lo largo de la cual se insertan los otros puntos, los puntos finales de las abscisas. Si, por ejemplo, para llegar a la ecuación del círculo, elegimos cualquier punto de la periferia como punto cero, entonces la línea de las abscisas debe pasar por el centro del círculo. Todo esto encuentra igualmente aplicación en la mecánica, donde igualmente en el cálculo de los movimientos el punto tomado como cero en cada caso constituye el punto principal y pivote de toda la operación. El punto cero del termómetro es el límite inferior muy definido de la sección de temperatura que se divide en cualquier número deseado de grados, sirviendo así como una medida tanto para las etapas de temperatura dentro de la sección como también para temperaturas más altas o más bajas. De ahí que en este caso también sea un punto muy esencial. E incluso el cero absoluto del termómetro no representa en modo alguno una negación abstracta pura, sino un estado muy definido de la materia: el límite en el que se desvanece el último rastro de movimiento molecular independiente y la materia actúa sólo como masa. Dondequiera que nos encontremos con el cero

Cero poderes. De importancia en la serie logarítmica:

Todas las variables pasan en algún lugar por la unidad; por tanto, también una constante elevada a una potencia variable ( a ^x ) = 1, si x = 0. a ⁰ = 1 no significa más que concebir la unidad en su conexión con los demás miembros de la serie de potencias de a, solo que ahí tiene algún significado y puede conducir a resultados ( S x ⁰ = x / w ) ^[214], de lo contrario no en absoluto. De esto se sigue que también la unidad, por mucho que parezca idéntica a sí misma, incluye en sí una multiplicidad infinita, ya que puede ser la potencia cero de cualquier otro número posible, y que esta multiplicidad no es meramente imaginaria se prueba en cada ocasión. donde la unidad se concibe como una unidad determinada, como uno de los resultados variables de un proceso (como una magnitud momentánea o forma de una variable) en conexión con este proceso.

* * *

√ — 1. Las magnitudes negativas del álgebra son reales sólo en la medida en que están conectadas con magnitudes positivas y sólo dentro de la relación con estas últimas; fuera de esta relación, tomados por sí mismos, son puramente imaginarios. En trigonometría y geometría analítica, junto con las ramas de las matemáticas superiores de las que estas son la base, expresan una dirección de movimiento definida, opuesta a la dirección positiva. Pero el seno y la tangente del círculo se pueden calcular desde el cuadrante superior derecho al igual que desde el cuadrante inferior derecho, invirtiendo así directamente más y menos. De manera similar, en geometría analítica, las abscisas se pueden calcular desde la periferia o desde el centro del círculo; de hecho, en todas las curvas se pueden calcular a partir de la curva en la dirección generalmente denotada como menos, (o) en cualquier dirección deseada, y aún así dar una ecuación racional correcta de la curva. Aquí, el más existe solo como el complemento de menos, y viceversa. Pero la abstracción algebraica las trata (magnitudes negativas) como reales e independientes, incluso fuera de la relación con unmayor magnitud positiva.

* * *

Matemáticas. Al sentido común le parece un absurdo resolver una magnitud definida, por ejemplo, una expresión binomial, en una serie infinita, es decir, en algo indefinido. Pero, ¿dónde estaríamos sin las series infinitas y el teorema del binomio?

Asíntotas. La geometría comienza con el descubrimiento de que lo recto y lo curvo son opuestos absolutos, que lo recto es absolutamente inexpresable en lo curvo y lo curvo en lo recto, que los dos son inconmensurables. Sin embargo, incluso el cálculo del círculo solo es posible expresando su periferia en líneas rectas. Para las curvas con asíntotas, sin embargo, la recta se fusiona completamente con la curva y la curva en la recta, tanto como la noción de paralelismo: las líneas no son paralelas, se acercan continuamente entre sí y, sin embargo, nunca se encuentran; el brazo de la curva se vuelve cada vez más recto, sin llegar a serlo del todo, al igual que en la geometría analítica la línea recta se considera una curva de primer orden con una curvatura infinitamente pequeña. Por grande que sea la x de la curva logarítmica, y nunca puede = 0.

* * *

Recto y curvo en el cálculo diferencial se ponen en último recurso como iguales: en el triángulo diferencial, cuya hipotenusa forma el diferencial del arco (en el método de la tangente), esta hipotenusa puede considerarse

“Como una línea pequeña, bastante recta, que es al mismo tiempo el elemento del arco y el de la tangente” – no importa si la curva se considera compuesta de un número infinito de líneas rectas, o también, “si se considera como una curva estricta; dado que la curvatura en cada punto M es infinitamente pequeña, la última relación del elemento de la curva al de la tangente es evidentemente una relación de igualdad «.

Aquí, por lo tanto, aunque la razón se acerca continuamente a la igualdad, pero asintóticamente de acuerdo con la naturaleza de la curva, sin embargo, dado que el contacto se limita a un solo punto que no tiene longitud, finalmente se asume que la igualdad de la recta y la curva ha sido alcanzado. (Bossut, Calcul différentiel et intégral, París, An VI, 1, p. 149.) ^[215] En curvas polares ^[216]las abscisas imaginarias diferenciales incluso se toman como paralelas a las abscisas reales y las operaciones basadas en esta, aunque ambas se encuentran en el polo; de hecho, de ella se deduce la semejanza de dos triángulos, uno de los cuales tiene un ángulo precisamente en el punto de intersección de las dos líneas, ¡cuyo paralelismo es la base total de la semejanza! (Figura 17.) ^[217]

Cuando las matemáticas de las líneas rectas y curvas han llegado al agotamiento, las matemáticas abren un nuevo campo casi infinito que concibe la curva como recta (el triángulo diferencial) y la recta como curva (curva de primer orden con curvatura infinitamente pequeña). . ¡Oh metafísica!

* * *

Trigonometría. Una vez que la geometría sintética ha agotado las propiedades de un triángulo, considerado como tal, y no tiene nada nuevo que decir, se abre un horizonte más extenso mediante un procedimiento muy simple y completamente dialéctico. El triángulo ya no se considera en sí mismo, sino en conexión con otra figura, el círculo. Cada triángulo rectángulo puede considerarse como perteneciente a un círculo: si la hipotenusa = r, entonces los lados que encierran el ángulo recto son sin y cos; si uno de estos lados = r,luego el otro = bronceado, la hipotenusa = seg. De esta manera, los lados y los ángulos reciben relaciones definidas bastante diferentes que sin esta relación del triángulo con el círculo sería imposible de descubrir y usar, y surge una teoría del triángulo bastante nueva, que supera con creces la antigua y universalmente aplicable. porque cada triángulo se puede resolver en dos triángulos rectángulos. Este desarrollo de la trigonometría a partir de la geometría sintética es un buen ejemplo de dialéctica, de la forma en que comprende las cosas en su interconexión en lugar de de forma aislada.

* * *

Identidad y diferencia : la relación dialéctica ya se ve en el cálculo diferencial, donde dx es infinitamente pequeño, pero es efectivo y lo hace todo.

* * *

Molécula y diferencial . Wiedemann (III, p. 636) ^[218] pone distancias finitas y moleculares en oposición directa entre sí.

Sobre los prototipos del infinito matemático en el mundo real =
Re pp. 17-18. ^[219] Concordancia de pensamiento y ser. – El infinito en matemáticas

El hecho de que nuestro pensamiento subjetivo y el mundo objetivo estén sujetos a las mismas leyes, y por tanto, también, que en el análisis final no puedan contradecirse en sus resultados, sino que deban coincidir, gobierna absolutamente todo nuestro pensamiento teórico. Es la premisa inconsciente e incondicional del pensamiento teórico. El materialismo del siglo XVIII, por su carácter esencialmente metafísico, investigó esta premisa sólo en lo que respecta al contenido. Se limitó a demostrar que el contenido de todo pensamiento y conocimiento debe derivar de la experiencia sensorial y revivió el principio: nihil est in intellectu, quod non fuerit in sensu . ^[220]Era la filosofía moderna idealista, pero al mismo tiempo dialéctica, y especialmente Hegel, que por primera vez la investigaba también en lo que respecta a la forma. A pesar de todas las innumerables construcciones arbitrarias y fantasías que encontramos aquí, a pesar de la forma idealista y al revés de su resultado -la unidad de pensamiento y ser-, es innegable que esta filosofía demostró la analogía de los procesos del pensamiento. a los de la naturaleza e historia y viceversa, y la vigencia de leyes similares para todos estos procesos, en numerosos casos y en los más diversos campos. Por otro lado, la ciencia natural moderna ha ampliado el principio del origen de todo el contenido del pensamiento a partir de la experiencia de una manera que rompe su antigua formulación y limitación metafísica. Al reconocer la herencia de los caracteres adquiridos, se extiendeel tema de la experiencia del individuo al género; el individuo único que debe tener experiencia ya no es necesario, su experiencia individual puede ser reemplazada hasta cierto punto por los resultados de las experiencias de varios de sus antepasados. Si, por ejemplo, entre nosotros los axiomas matemáticos le parecen evidentes a todos los niños de ocho años, y no necesitan pruebas de la experiencia, esto es únicamente el resultado de la «herencia acumulada». Sería difícil enseñarles mediante una prueba a un bosquimano o un negro australiano.

En el presente trabajo [ Anti-Dühring ] la dialéctica se concibe como la ciencia de las leyes más generales de todo movimiento. Esto implica que sus leyes deben ser válidas tanto para el movimiento en la naturaleza y la historia humana como para el movimiento del pensamiento. Tal ley puede ser reconocida en dos de estas tres esferas, incluso en las tres, sin que el filisteo metafísico se dé cuenta claramente de que es una y la misma ley que ha llegado a conocer.

Tomemos un ejemplo. De todos los avances teóricos, seguramente no hay ninguno que se ubique tan alto como un triunfo de la mente humana como el descubrimiento del cálculo infinitesimal en la última mitad del siglo XVII. Si en algún lugar, es aquí donde tenemos una proeza pura y exclusiva de la inteligencia humana. El misterio que aún hoy envuelve las magnitudes empleadas en el cálculo infinitesimal, los diferenciales e infinitos de varios grados, es la mejor prueba de que todavía se imagina que lo que aquí se trata son puras “creaciones e imaginaciones libres” ”de lo humano. mente, a la que no hay nada que corresponda en el mundo objetivo, pero al contrario, la naturaleza ofrece prototipos para todas estas magnitudes imaginarias.

Nuestra geometría toma como punto de partida las relaciones espaciales, y nuestras magnitudes numéricas aritméticas y de álgebra, que corresponden a nuestras condiciones terrestres, que por lo tanto corresponden a la magnitud de los cuerpos que la mecánica denomina masas-masas como las que ocurren en la Tierra y son movidas por los hombres. . En comparación con estas masas, la masa de la tierra parece infinitamente grande y, de hecho, la mecánica terrestre la trata como infinitamente grande. El radio de la tierra == oo, este es el principio básico de toda mecánica en la ley de caída. Pero nosimplemente la tierra, pero todo el sistema solar y las distancias que ocurren en este último a su vez parecen infinitamente pequeñas tan pronto como tenemos que tratar con las distancias calculadas en años luz en el sistema estelar visible para nosotros a través del telescopio. Tenemos aquí, por tanto, ya un infinito, no sólo de primer grado sino de segundo grado, y podemos dejar a la imaginación de nuestros lectores la construcción de infinitos ulteriores de grado superior en el espacio infinito, si se sienten inclinados a hacerlo. entonces.

Sin embargo, según la visión que prevalece en la física y la química hoy en día, las masas terrestres, los cuerpos con los que opera la mecánica, constan de moléculas, de partículas más pequeñas que no pueden dividirse más sin abolir la identidad física y química del cuerpo en cuestión. Según los cálculos de W. Thomson, el diámetro de la más pequeña de estas moléculas no puede ser menor que la cincuenta millonésima parte de un milímetro. ^[221]Pero incluso si asumimos que la molécula más grande en sí alcanza un diámetro de veinticinco millonésimas de milímetro, sigue siendo una magnitud infinitesimalmente pequeña en comparación con la masa más pequeña de la que se ocupan la mecánica, la física o incluso la química. Sin embargo, está dotado de todas las propiedades propias de la masa en cuestión, puede representar la masa física y químicamente, y realmente la representa en todas las ecuaciones químicas. En resumen, tiene las mismas propiedades en relación con la masa correspondiente que tiene el diferencial matemático en relación con sus variables. La única diferencia es que lo que nos parece misterioso e inexplicable en el caso del diferencial, en la abstracción matemática, aquí parece natural y por así decirlo obvio.

La naturaleza opera con estos diferenciales, las moléculas, exactamente de la misma manera y de acuerdo con las mismas leyes que las matemáticas con sus diferenciales abstractos. Así, por ejemplo, el diferencial de x ³ = 3 x ² dx, donde 3 x dx ² y dx ³están descuidados. Si ponemos esto en forma geométrica, tenemos un cubo con lados de longitud x, la longitud se incrementa en la cantidad infinitamente pequeña dx. Supongamos que este cubo consta de un elemento sublimado, digamos azufre; y que tres de las superficies alrededor de una esquina estén protegidas y las otras tres libres. Expongamos ahora este cubo de azufre a una atmósfera de vapor de azufre y bajemos suficientemente la temperatura; El azufre se depositará en los tres lados libres del cubo. Nos mantenemos completamente dentro del modo ordinario de procedimiento de la física y la química al suponer, para representar el proceso en su forma pura, que en primer lugar se deposita una capa del espesor de una sola molécula en cada uno de estos tres lados. La longitud xde los lados del cubo ha aumentado en el diámetro de una molécula dx. El contenido del cubo x ³ ha aumentado por la diferencia entre x ³ y x ³ +3 x ² dx + 3 x dx ² + d x ³ , donde dx ³ , una sola molécula, y 3 x dx ² , tres filas de la longitud x + dx, que consiste simplemente en moléculas dispuestas linealmente, puede despreciarse con la misma justificación que en matemáticas. El resultado es el mismo, el aumento de masa del cubo es 3 x ² dx.

Estrictamente hablando, dx ³ y 3 x dx ² no ocurren en el caso del cubo de azufre, porque dos o tres moléculas no pueden ocupar el mismo espacio, y el aumento de volumen del cubo es por lo tanto exactamente 3 x ² dx + 3 x dx + dx . Esto se explica por el hecho de que en matemáticas dx es una magnitud lineal, mientras que es bien sabido que tales líneas, sin espesor ni amplitud, no ocurren de forma independiente en la naturaleza, por lo que también las abstracciones matemáticas tienen validez irrestricta solo en matemáticas puras. Y dado que este último descuida 3xdx ² + dx ³ , no hay diferencia.

Similarmente en la evaporación. Cuando la capa molecular superior en un vaso de agua se evapora, la altura de la capa de agua, x, disminuye en dx, y el vuelo continuo de una capa molecular tras otra es en realidad una diferenciación continua. Y cuando el vapor caliente se condensa una vez más en agua en un recipiente por presión y enfriamiento, y una capa molecular se deposita sobre otra (está permitido dejar de lado las circunstancias secundarias que hacen que el proceso sea impuro) hasta que el recipiente sea completa, entonces literalmente se ha realizado una integración que se diferencia de la matemática sólo en que una es realizada conscientemente por el cerebro humano, mientras que la otra es realizada inconscientemente por la naturaleza.

Pero no es sólo en la transición del estado líquido al gaseoso y viceversa donde ocurren procesos completamente análogos a los del cálculo infinitesimal. Cuando el movimiento de masas, como tal, es abolido -por el impacto- y se transforma en calor, movimiento molecular, ¿qué sucede sino que el movimiento de masas se diferencia? Y cuando los movimientos de las moléculas de vapor en el cilindro de la máquina de vapor se suman de modo que elevan el pistón en una cantidad definida, de modo que se transforman en movimiento de masa, ¿no se han integrado? La química disocia moléculas en átomos, magnitudes de menor masa y extensión espacial, pero magnitudes del mismo orden, de modo que las dos están en relaciones definidas y finitas entre sí. Por lo tanto, todas las ecuaciones químicas que expresan la composición molecular de los cuerpos están en su forma ecuaciones diferenciales. Pero en realidad ya están integrados debido a los pesos atómicos que figuran en ellos. Para los cálculos de química con diferenciales, se conoce la relación mutua de cuyas magnitudes.

Los átomos, sin embargo, no se consideran en modo alguno simples o, en general, como las partículas de materia más pequeñas conocidas. Aparte de la química misma, que se inclina cada vez más a considerar que los átomos son compuestos, la mayoría de los físicos afirman que el éter universal, que transmite radiaciones de luz y calor, también consta de partículas discretas, que, sin embargo, son tan pequeñas que tienen la misma relación con los átomos químicos y las moléculas físicas que estas con las masas mecánicas, es decir, como d ² x a dx. Aquí, por lo tanto, en la noción ahora habitual de la constitución de la materia, tenemos igualmente un diferencial de segundo grado, y no hay ninguna razón en absoluto por la cual alguien, a quien daría satisfacción, no debería imaginar que las analogías de d ³ x, d ⁴x, etc., también ocurren en la naturaleza.

Por tanto, cualquiera que sea el punto de vista que uno pueda tener sobre la constitución de la materia, es cierto que está dividida en una serie de grupos grandes y bien definidos de un carácter de masas relativamente diferente de tal manera que los miembros de cada grupo separado se colocan entre sí en proporciones de masa finitas definidas, en contraste con las que los del siguiente grupo se sitúan en la proporción de lo infinitamente grande o infinitamente pequeño en el sentido matemático. El sistema visible de estrellas, el sistema solar, masas terrestres, moléculas y átomos, y finalmente las partículas de éter, forman cada uno de ellos tal grupo. No altera el caso de que se puedan encontrar vínculos intermedios entre los grupos separados. Así, entre las masas del sistema solar y las masas terrestres se encuentran los asteroides (algunos de los cuales tienen un diámetro no mayor que, por ejemplo,^[222] ), meteoritos, etc. Así, en el mundo orgánico la célula se encuentra entre masas y moléculas terrestres. Estos vínculos intermedios sólo prueban que no hay saltos en la naturaleza, precisamente porque la naturaleza está compuesta enteramente por saltos.

En la medida en que las matemáticas calculan con magnitudes reales, también emplean este modo de perspectiva sin dudarlo. Para la mecánica terrestre, la masa de la tierra se considera infinitamente grande, al igual que para la astronomía, las masas terrestres y los meteoritos correspondientes a ellas se consideran infinitamente pequeños, y así como las distancias y masas de los planetas del sistema solar se reducen a nada cuando tan pronto como la astronomía investigue la constitución de nuestro sistema estelar que se extiende más allá de las estrellas fijas más cercanas. Sin embargo, tan pronto como los matemáticos se retiran a su inexpugnable fortaleza de abstracción, las llamadas matemáticas puras, todas estas analogías se olvidan, el infinito se convierte en algo totalmente misterioso y la forma en que se llevan a cabo las operaciones con él en el análisis aparece como algo. absolutamente incomprensible, contradiciendo toda experiencia y toda razón. Las estupideces y absurdos con los que los matemáticos han excusado más que explicado su modo de proceder, que sorprendentemente siempre conduce a resultados correctos, exceden las peores fantasías aparentes y reales, por ejemplo, de la filosofía hegeliana de la naturaleza, acerca de la cual los matemáticos y los científicos naturales pueden. nunca expresar adecuadamente su horror. Lo que acusan a Hegel de hacer, es decir, llevar las abstracciones al límite extremo, lo hacen ellos mismos en una escala mucho mayor. Olvidan que toda la llamada matemática pura se ocupa de abstracciones, que todas sus magnitudes, estrictamente hablando, son imaginarias, y que todas las abstracciones, cuando se las lleva al extremo, se transforman en sinsentidos o en su contrario. El infinito matemático se toma de la realidad, aunque inconscientemente, y por tanto sólo puede explicarse desde la realidad y no desde sí misma, desde la abstracción matemática. Y, como hemos visto, si investigamos la realidad a este respecto, llegamos también a las relaciones reales de las que se toma la relación matemática del infinito, e incluso a las analogías naturales del modo matemático en que opera esta relación. Y así se explica el asunto.

(Mala reproducción de Haeckel de la identidad del pensamiento y el ser. Pero también la contradicción entre materia continua y discreta; ver Hegel.) ^[223]

* * *

El cálculo diferencial por primera vez hace posible que las ciencias naturales representen matemáticamente procesos y no solo estados: movimiento.

* * *

Aplicación de las matemáticas: en la mecánica de cuerpos sólidos es absoluta, en la de gases aproximada, en la de fluidos ya más difícil; en física más provisional y relativo; en química, ecuaciones simples de primer orden y de la más simple naturaleza; en biología = 0

Notas

213. En el primer caso, Engels tiene en mente la observación de Hegel de que en aritmética el pensamiento se mueve en la “irreflexión” ( Ciencia de la lógica , Libro I, Sección II, Capítulo 2, Observación sobre el empleo de determinaciones numéricas para expresar conceptos filosóficos); en el último caso, la afirmación de Hegel de que “ya el sistema numérico natural ejemplifica una línea nodal de momentos cualitativos, que se manifiestan en la progresión meramente externa”, etc. (ibid., Sección III, Capítulo 2, Observación sobre ejemplos de líneas nodales de relaciones de medida; natura non facit saltum ).

214. Esta expresión se da en el libro de Bossut, al que se refiere Engels en el fragmento “Straight and Curved”. En el capítulo sobre «Cálculo integral con diferencias finitas», Bossut examina en primer lugar el siguiente problema: «Integrar o sumar los pasos de números enteros de una variable de magnitud x «. Bossut asume que la diferencia D x es constante y la denota con la letra griega w . Dado que la suma de D x o de w es igual ax , la suma de w × 1 o de w x ⁰ también es igual ax . Bossut escribe esta ecuación en la forma Sw x ⁰= x . Bossut luego saca la constante w y la pone antes del signo de suma, obteniendo la expresión wS x ⁰ = x , de x / w, de la cual obtiene la ecuación S x ⁰ = w / w . Luego, Bossut usa esta última ecuación para encontrar las magnitudes S x, S x ² , S x ³ , etc., para resolver otros problemas. Véase Bossut, Traités de Calcul differentiel et de Calcul integral , t. 1, París, 1798, pág. 38.

215. Cap. Bossut, Traités de Calcul differentiel et de Calcul intégral , t. I, Paris, an VI (1798), pág. 149.

216. Así es como Bossut denomina las curvas consideradas en el sistema de coordenadas polares.

217. Engels tiene en mente la figura 17 y su explicación en las páginas 148-51 del Tratado de Bossut. Esta figura tiene la siguiente forma: BMK es la curva. MT es su tangente. P es el polo u origen de las coordenadas. PZ es el eje polar. PM es la ordenada del punto M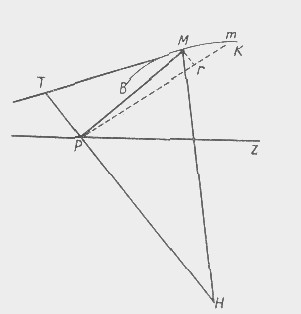 

(Engels lo llama “abscisa real”; hoy en día se llama radio-vector). Pm es la ordenada del punto m que se encuentra infinitamente cerca de M (Engels llama a este radio-vector la “abscisa imaginaria diferencial”). MH , perpendicular a la tangente MT . TPH , perpendicular a la ordenada PM . Señor, la curva descrita por el radio PM. Como MPm – es un ángulo infinitesimal, PM y Pm se consideran paralelos. Los triángulos Mrm y TPM , así como también los triángulos Mrm y MPH , son. considerado similar.

218. Ver nota 95.

219. Esta nota es una de las tres notas más grandes ( Noten ) que Engels puso en la segunda carpeta de materiales de Dialéctica de la naturaleza.

(Ver Nota 204.) Fue escrito originalmente como el primer esbozo de una nota de comentario de las páginas 17-18 de la primera edición de [Anti] -Dühring.

El título “Sobre los prototipos del infinito matemático en el mundo real” lo dio Engels en la lista de contenidos de la segunda carpeta de Dialéctica de la naturaleza. El subtítulo “A las págs. 17-18; Concordancia de pensamiento y ser. – El Infinito en Matemáticas ”se encuentra al principio de la nota.

220. Nihil est in intellectu, quod non fuerit in sensu (no hay nada en la mente que no haya estado en los sentidos), el principio fundamental del sensualismo. El contenido de esta fórmula se remonta a Aristóteles (ver su Análisis posterior).

221. Esta cifra se da en un artículo de William Thomson, titulado «El tamaño de los átomos», que se publicó por primera vez en la revista Nature No. 22, del 31 de marzo de 1870, y luego se reimprimió como apéndice en la segunda edición de Tratado sobre filosofía natural de Thomson y Tait (Vol. 1, Parte II, nueva ed., Cambridge, 1883, págs. 501-52).

222. Uno de los estados enanos que forman parte del Imperio Alemán desde 1871.

223. Aquí Engels posiblemente tenga en mente el monismo psicofísico de Haeckel y sus puntos de vista sobre la estructura de la materia. En Die Perigenesis der Plastidule (La perigénesis del plastidule), que Engels cita en su Segunda nota a [Anti] -Dühring (véase la presente edición, pág. no solo en «plastidules» o moléculas de protoplasma, sino también en átomos, y que todos los átomos son «animados» y poseen «sensación» y «volición». En el mismo libro, Haeckel describe los átomos como algo absolutamente discreto, absolutamente indivisible y absolutamente inalterable, mientras que junto con los átomos discretos reconoce la existencia del éter como algo absolutamente continuo (op. Cit., Berlín, 1876, S. 38-40).

Engels menciona en su nota «La divisibilidad de la materia» (véase la presente edición, p. 245) cómo Hegel trata la contradicción de la continuidad y la discreción de la materia.