BICENTENARIO DE NACIMIENTO FEDERICO ENGELS 1820
VIII: Fricción de las mareas, Kant y Thomson-Tait sobre la rotación de la Tierra y la atracción lunar
THOMSON y Tait, Nat. Philos. , Yo, p. 191 (párrafo .276):
«También existen resistencias indirectas, por fricciones que impiden el movimiento de las mareas, en todos los cuerpos que, como la tierra, tienen partes de sus superficies libres cubiertas por líquido, que, mientras estos cuerpos se muevan relativamente a los cuerpos vecinos, deben seguir dibujando energía de sus movimientos relativos. Así, si consideramos, en primer lugar, la acción de la luna sola, en la tierra con sus océanos, lagos y ríos, percibimos que debe tender a igualar los períodos de la tierra rotación alrededor de su eje, y de la revolución de los dos cuerpos alrededor de su centro de inercia; porque mientras estos períodos difieran, la acción de las mareas de la superficie terrestre debe seguir restando energía a sus movimientos. Para ver el tema con más detalle, y, al mismo tiempo, evitar complicaciones innecesarias,supongamos que la luna es un cuerpo esférico uniforme, la acción y reacción mutua de la gravitación entre su masa y la de la tierra será equivalente a una sola fuerza en alguna línea a través de su centro;y debe ser tal que impida la rotación de la tierra siempre que se realice en un período más corto que el movimiento de la luna alrededor de la tierra . Por lo tanto, debe estar en alguna dirección como la línea MQ del diagrama, que representa, necesariamente con enorme exageración, su desviación, OQ, del centro de la Tierra. Ahora bien, se puede considerar que la fuerza real sobre la luna en la línea MQ consiste en una fuerza en la línea MO hacia el centro de la tierra, sensiblemente igual en cantidad a la fuerza total, y una fuerza comparativamente muy pequeña en la línea MT perpendicular a MO . Este último es casi tangencial al camino de la luna, y está en la dirección consu movimiento. Tal fuerza, si de repente comenzara a actuar, aumentaría, en primer lugar, la velocidad de la luna; pero después de cierto tiempo se habría alejado tanto de la tierra, en virtud de esta aceleración, que habría perdido, moviéndose contra la atracción de la tierra,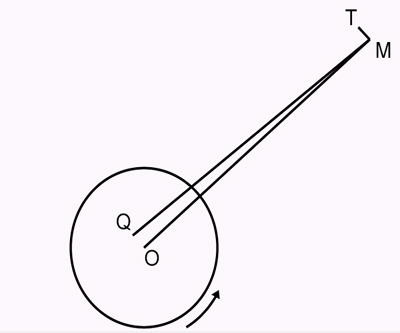 
tanta velocidad como había ganado por la fuerza de aceleración tangencial. El efecto de una fuerza tangencial continua, que actúa con el movimiento, pero en una cantidad tan pequeña como para hacer solo una pequeña desviación en cualquier momento de la forma circular de la órbita, es aumentar gradualmente la distancia desde el cuerpo central y causar tanto como su propia cantidad de trabajo a realizar contra la atracción de la masa central, por la energía cinética del movimiento perdido. Las circunstancias se entenderán fácilmente si se considera este movimiento alrededor del cuerpo central en una trayectoria en espiral muy gradual que tiende hacia afuera. Siempre que el La ley de la fuerza es el cuadrado inverso de la distancia, la componente tangencial de la gravedad contra el movimiento será dos veces mayor que la fuerza tangencial perturbadora en la dirección del movimiento; y por lo tanto, la mitad del trabajo realizado contra el primero, lo realiza el segundo, y la otra mitad por la energía cinética extraída del movimiento. El efecto integral sobre el movimiento de la luna, de la causa perturbadora particular que ahora estamos considerando, se encuentra más fácilmente utilizando el principio de los momentos de los momentos. Así vemos que tanto momento de impulso se gana en cualquier tiempo por los movimientos de los centros de inercia, de la luna y la tierra con respecto a su centro común de inercia, como se pierde por la rotación de la tierra alrededor de su eje.
El plano medio del primero es la eclíptica; y por lo tanto los ejes de los dos momentos están inclinados entre sí en el ángulo promedio de 23 ° 27,5 ‘ , que, como estamos descuidando la influencia del sol en el plano del movimiento de la luna, puede tomarse como la inclinación real de los dos. ejes en la actualidad. El momento resultante, o el momento total, es por lo tanto 5,38 veces el de la rotación actual de la Tierra, y su eje está inclinado 19 ° 13 ‘ con respecto al eje de la Tierra. De ahí la última tendencia de las mareases reducir la tierra y la luna a una simple rotación uniforme con este momento resultante alrededor de este eje resultante, como si fueran dos partes de un cuerpo rígido: en cuya condición la distancia de la luna aumentaría (aproximadamente) en la proporción 1: 1,46 , siendo la relación entre el cuadrado del momento presente de impulso de los centros de inercia y el cuadrado de todo el momento de impulso; y el período de revolución en la relación 1: 1,77, siendo el de los cubos de las mismas cantidades. Por tanto, la distancia se incrementaría a 847.100 millas y el período se alargaría a 48,36 días. ¿No había otro cuerpo en el universo, sino la tierra y la luna, estos dos cuerpos podrían seguir moviéndose así para siempre, en órbitas circulares alrededor de su centro común de inercia, y la tierra girando alrededor de su eje en el mismo período, de modo que siempre gire la misma cara hacia la luna y, por lo tanto, tener todos los líquidos en su superficie en reposo en relación con el sólido. Pero la existencia del sol evitaría que tal estado de cosas fuera permanente. Habría mareas solares – el doble de marea alta y el doble de marea baja – en el período de la revolución de la tierra con relación al sol (es decir, dos veces en el día solar, o lo que sería lo mismo, el mes). Esto no podría continuar sin pérdida de energía por la fricción del fluido.. No es fácil rastrear el curso completo de la perturbación en los movimientos de la tierra y la luna que produciría esta causa, pero su efecto final debe ser hacer que la tierra, la luna y el sol giren alrededor de su centro común de inercia, como partes. de un cuerpo rígido «. [1]
Kant, en 1754, fue el primero en plantear la opinión de que la rotación de la tierra se retarda por la fricción de las mareas y que este efecto solo llegará a su conclusión «cuando su superficie (la de la tierra) esté en reposo relativo en relación con la luna, es decir , cuando girará sobre su eje en el mismo período que la luna tarda en girar alrededor de la tierra, y en consecuencia siempre girará del mismo lado a esta última ”. Sostuvo la opinión de que este retraso tenía su origen solo en la fricción de las mareas, que surge, por lo tanto, de la presencia de masas fluidas en la tierra:
«Si la tierra fuera una masa bastante sólida sin ningún fluido, ni la atracción del sol ni de la luna haría nada para alterar su rotación axial libre; porque atrae con igual fuerza las partes este y oeste de la esfera terrestre y por lo tanto, no causa ninguna inclinación ni hacia uno ni hacia el otro lado; en consecuencia, permite a la tierra plena libertad para continuar esta rotación sin obstáculos como si no hubiera influencia externa sobre ella «.
Kant podría contentarse con este resultado. En ese momento faltaban todos los prerrequisitos científicos para penetrar más profundamente en el efecto de la luna en la rotación de la tierra. De hecho, se necesitaron casi cien años antes de que la teoría de Kant obtuviera un reconocimiento general, y aún más antes de que se descubriera que el reflujo y el flujo de las mareas son solo el aspecto visible del efecto ejercido por la atracción del sol y la luna en la rotación de la tierra.
Esta concepción más general del asunto es precisamente la que han desarrollado Thomson y Tait. La atracción de la luna y el sol afecta no solo a los fluidos del cuerpo terrestre o su superficie, sino a toda la masa de la tierra en general de una manera que dificulta la rotación de la tierra. Mientras el período de rotación de la tierra no coincida con el período de la revolución de la luna alrededor de la tierra, mientras la atracción de la luna, para tratar esto solo en primer lugar, tiene el efecto de acercar y acercar los dos períodos. más juntos. Si el período de rotación del cuerpo central (relativo) fuera más largo que el período de revolución de. el satélite, el primero se iría alargando gradualmente; [2]si fuera más corto, como es el caso de la Tierra, se ralentizaría. Pero ni en un caso la energía cinética se creará de la nada, ni en el otro será aniquilada. En el primer caso, el satélite se acercaría más al cuerpo central y acortaría su período de revolución, en el segundo aumentaría su distancia de él y adquiriría un período de revolución más largo. En el primer caso, el satélite al acercarse al cuerpo central pierde exactamente la misma energía potencial a medida que el cuerpo central gana energía cinética a partir de la rotación acelerada; en el segundo caso, el satélite, al aumentar su distancia, gana exactamente la misma cantidad de energía potencial que el cuerpo central pierde en energía cinética de rotación. La cantidad total de energía dinámica, potencial y cinética, presente en el sistema Tierra-Luna sigue siendo la misma; el sistema es completamente conservador. [3]
Se ve que esta teoría es completamente independiente de la constitución físico-química de los cuerpos en cuestión. Se deriva de las leyes generales del movimiento de los cuerpos celestes libres, produciéndose la conexión entre ellos por atracción en proporción a sus masas e inversamente proporcional al cuadrado de las distancias entre ellos. Evidentemente, la teoría ha surgido como una generalización de la teoría de la fricción de las mareas de Kant, e incluso Thomson y Tait la presentan aquí como su fundamentación en líneas matemáticas. Pero en realidad, y sorprendentemente los autores simplemente no tienen ni idea de esto, en realidad excluye el caso especial de la fricción de las mareas.
La fricción es un obstáculo para el movimiento de la masa y durante siglos se consideró como la destrucción de dicho movimiento y, por tanto, de la energía cinética. Ahora sabemos que la fricción y el impacto son las dos formas en las que la energía cinética se convierte en energía molecular, en calor. En toda fricción, por tanto, la energía cinética como tal se pierde para reaparecer, no como energía potencial en el sentido de la dinámica, sino como movimiento molecular en la forma definida de calor. Por tanto, la energía cinética perdida por fricción se pierde realmente en primer lugar para los aspectos dinámicos del sistema en cuestión. Solo puede volver a ser dinámicamente efectivo si se vuelve a convertir de la forma de calor en energía cinética.
¿Cómo está entonces la cuestión en el caso de la fricción de las mareas? Es obvio que aquí también la totalidad de la energía cinética comunicada a las masas de agua en la superficie de la tierra por atracción lunar se convierte en calor, ya sea por fricción de las partículas de agua entre sí en virtud de la viscosidad del agua, o por fricción en la superficie rígida de la tierra y la conminución de rocas que se levantan contra el movimiento de las mareas. De este calor sólo se reconvierte en energía cinética la parte infinitesimalmente pequeña que contribuye a la evaporación en la superficie del agua. Pero incluso esta cantidad infinitesimalmente pequeña de energía cinética, que deja el sistema total tierra-luna en una parte de la superficie terrestre, permanece en primer lugar sujeta a las condiciones que prevalecen en la superficie terrestre,
En consecuencia, en la medida en que la fricción de las mareas actúe indiscutiblemente de manera impedida sobre la rotación de la Tierra, la energía cinética utilizada para este propósito se pierde absolutamente para el sistema dinámico Tierra-Luna. Por tanto, no puede reaparecer dentro de este sistema como energía potencial dinámica. En otras palabras, de la energía cinética gastada en impedir la rotación de la tierra por medio de la atracción de la luna, solo la parte que actúa sobre el sólidoLa masa del cuerpo de la Tierra puede reaparecer por completo como energía potencial dinámica y, por lo tanto, ser compensada por un aumento correspondiente de la distancia de la luna. Por otro lado, la parte que actúa sobre las masas fluidas de la tierra sólo puede hacerlo en la medida en que no ponga a estas masas en un movimiento opuesto en la dirección al de la rotación de la tierra, ya que tal movimiento es totalmente se convierte en calor y finalmente se pierde en el sistema por radiación.
Lo que es válido para la fricción de las mareas en la superficie de la tierra es igualmente válido para la fricción de las mareas tan a menudo hipotéticamente asumida de un supuesto núcleo fluido del interior de la Tierra.
La parte más peculiar del asunto es que Thomson y Tait no se dan cuenta de que para establecer la teoría de la fricción de las mareas están proponiendo una teoría que parte del supuesto tácito de que la Tierra es un cuerpo completamente rígido , [4] y por lo tanto, excluya cualquier posibilidad de flujo de marea y, por lo tanto, también de fricción de marea.
Notas
1. Esta teoría se ha desarrollado mucho desde entonces y se ha encontrado aproximadamente la velocidad real a la que la fricción de las mareas alarga el día.
2. Un desliz del bolígrafo; la palabra obviamente debería ser «abreviada».
3.No cabe duda de que Engels tenía razón cuando señaló el error de Thomson y Tait al decir que los cambios en la duración del día y del mes «no podían continuar sin pérdida de energía por la fricción de los fluidos». Ahora sabemos que hay mareas tanto en la tierra como en el océano. Pero Engels se equivocó al suponer que la luna podría alejarse de la tierra sin pérdida de energía. Porque en un sistema como la Tierra y la Luna, el momento angular (momento del momento) permanece constante a menos que sea disminuido o aumentado por la acción de las mareas de algún cuerpo externo. Si se conservan tanto el impulso como la energía, no puede ocurrir una desaceleración sistemática. Esto se ve fácilmente en el caso simplificado en el que se supone que la luna gira en un círculo en el plano del ecuador terrestre. En este caso solo hay dos variables posibles, la duración del día y del mes. Pero mientras el momento del momento y la energía del sistema no cambien, tenemos dos ecuaciones para determinar estas cantidades y, por lo tanto, son fijas.
4. Aunque Engels formuló incorrectamente su crítica a Thomson y Tait, tenía razón en un punto fundamental. El sistema Tierra-Luna evolucionaría de tal manera que alargaría el día y el mes incluso si no hubiera océano. Porque la tierra es uncuerpo sólido ( enconado ), pero no rígido (más estrellado).) cuerpo en el sentido en que esta última palabra se usa en la mecánica teórica, es decir, un cuerpo cuya forma no es alterada por las fuerzas sobre él. Por supuesto, un cuerpo rígido es una abstracción matemática, como una superficie plana. No hay cuerpos perfectamente rígidos ni superficies planas. Y ahora se ha demostrado que la tierra sólida se dobla ligeramente a medida que varía la atracción de la luna. Hay mareas sólidas y mareas líquidas, aunque mucho más pequeñas. Éstos actúan de la misma manera que las mareas en el océano, aunque mucho más lentamente.
